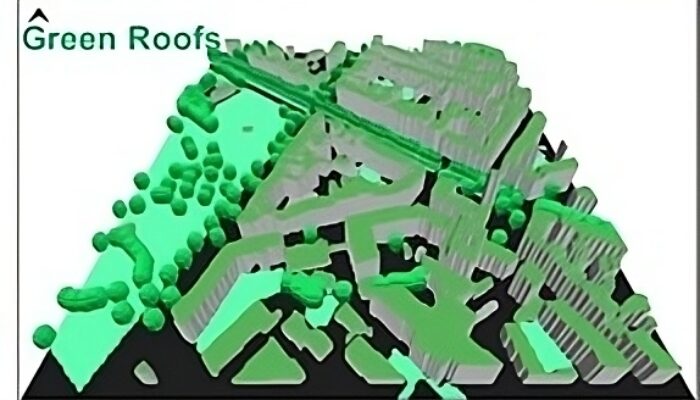
Urban areas often show higher temperatures than their surrounding rural areas, especially during heat events. This phenomenon is called the Urban Heat Island (UHI) effect. The magnitude of the UHI effect is expressed by the absolute temperature difference between the rural and the urban area and can reach more than 10 °C. During past decades, the magnitude of the UHI effect has intensified in many ...[Read More]
Spotlighting the Climate Division’s sessions for EGU24
Dear community of climate enthusiasts and EGU lovers, We know that being part of the EGU is not just about staying in the loop with the latest geoscience works – especially when it comes to our all-time favorite realm of sciences: climate sciences 🤩. It is also an amazing opportunity to spark exciting collaborations and expand your network with scientists from all over Europe and the world. EGU is ...[Read More]
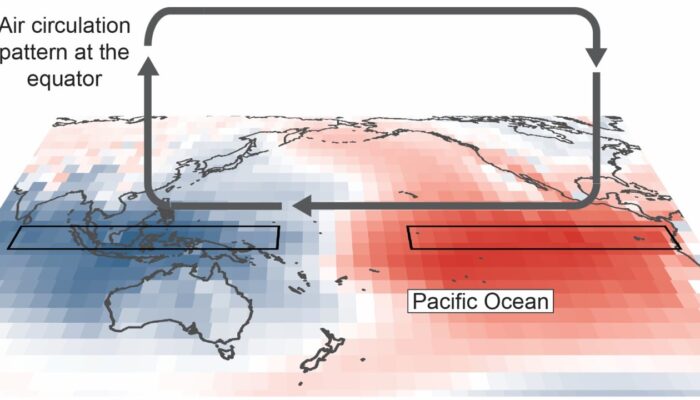
The Walker Circulation: what is it and why does it matter
What is the Walker Circulation? The El Niño Southern Oscillation, or ‘ENSO’, is one of the major causes of year to year variability in Earth’s climate. ENSO is characterised by: changes in the temperature of the ocean’s surface in the tropical Pacific Ocean, and by changes in atmospheric circulation in an east-west direction above the Pacific Ocean. Number two in that list is what makes ENS ...[Read More]
Why would anyone care about an ‘Anthropocene’?
– A debate among scientists and its impact on us The epoch of humans (and their obvious intervention in the Earth system) In order to understand what the ‘Anthropocene’ means for us, we need to define first what it actually is. This poses a rather complex question in itself, as various disciplines have given the term rather different and alternative definitions. For instance, the public medi ...[Read More]