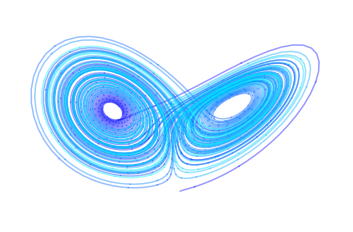
Since being immortalised in Hollywood film, “the butterfly effect” has become a commonplace concept, despite its obscure origins. Its name derives from an object known as the Lorenz attractor, which has the form of a pair of butterfly wings (Fig. 1). It is a portrait of chaos, the underlying principle hindering long-term weather prediction: just a small change in initial conditions leads to vastly different outcomes in the long run.
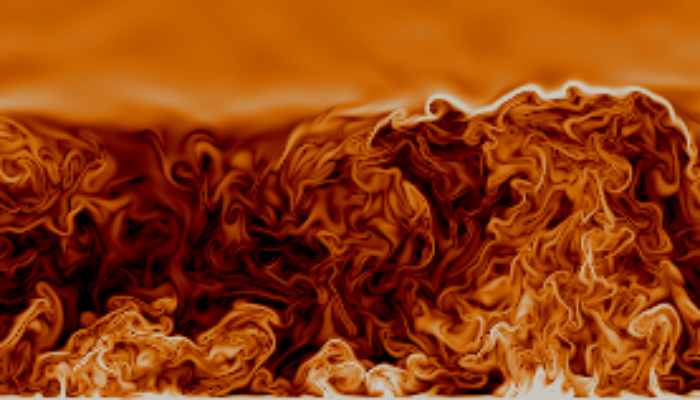
The three-equation system that gives rise to the Lorenz attractor is often referred to as a simple model of atmospheric convection, yet amongst the atmospheric science community, attention is rarely paid to the original fluid flow that the Lorenz equations describe. Consisting of a fluid layer heated from below and cooled from above, Rayleigh-Bénard convection (Fig. 2) is a hallmark flow beloved by fluid dynamicists and mathematicians alike for its analytical tractability, yet rich behaviour. It is often cited as being of immediate relevance for many geophysical and astrophysical flows [1]. The success of turbulent Rayleigh-Bénard convection in leading to our understanding of chaos, as exemplified by the Lorenz attractor, suggests the enticing possibility of gaining other key conceptual insights into the behaviour of the Earth’s atmosphere through the use of this simple convective system.
In a recent study [2] we explored this potential by investigating to what extent turbulent Rayleigh-Bénard convection serves as an analogue of the daytime atmospheric boundary layer, also known as the convective boundary layer (CBL). In particular, we investigated whether statistical properties in the surface layer develop with height in a similar way in both systems. The surface layer is typically just a few tens of metres thick, but due to the strong turbulent mixing that takes place there, it is of primary importance for the development of the boundary layer. The surface boundary conditions of Rayleigh-Bénard convection and the CBL are the same, which might lead one to think that surface-layer properties should behave similarly in both cases. However, differences in the upper boundary conditions between the two systems modify the large-scale circulations that appear in both systems and this may have an impact in the surface layer.
Indeed, despite the much-heralded relevance of Rayleigh-Bénard convection to geophysical flows, we find that its cooled upper plate modifies the large-scale structures in such a way that it substantially alters the behaviour of near-surface properties compared to the CBL. In particular, the downdrafts in Rayleigh-Bénard convection are considerably stronger than in the CBL and their impingement into the surface layer changes how velocity and temperature statistics develop with height.
However, we also find that just an incremental change to the upper boundary condition of Rayleigh-Bénard convection is needed to closely match surface-layer statistics in the CBL. If instead of being cooled, the upper plate is made adiabatic, i.e. no heat is allowed to escape (Fig. 3), the influence of the strong, cold downdrafts is removed, resulting in surface-layer similarity between this modified version of Rayleigh-Bénard convection and the CBL. Rayleigh-Bénard convection with an adiabatic top lid has the advantage that it is a simpler experimental set-up than the CBL and provides a longer statistically steady state, allowing for greater statistical convergence to be achieved through long-time averaging.
In the long term, the classical Rayleigh-Bénard system will continue to serve as a paradigm for studies of natural convection, though we are increasingly beginning to see that its practical application to geophysical and astrophysical [3] flows may not be as straightforward as past literature seems to suggest.
References
[1] A. Pandey, J. Scheel, and J. Schumacher. Turbulent superstructures in Rayleigh-Bénard convection.Nature Communications, 9:2118, 2018.
[2] K. Fodor, JP Mellado, and M. Wilczek. On the Role of Large-Scale Updrafts and Downdrafts in Deviations From Monin-Obukhov Similarity Theory in Free Convection. Boundary-Layer Meteorology, 2019.
[3] F. Wilczynski, D. Hughes, S. Van Loo, W. Arter, and F. Militello. Stability of scrape-off layer plasma: a modified Rayleigh-Bénard problem. Physics of Plasmas, 26:022510, 2019.
Edited by Dasaraden Mauree
 Katherine Fodor is a PhD. candidate at the Max Planck Institute for Meteorology in Hamburg, Germany. She uses very high resolution computer simulations to study turbulence in the atmosphere. In particular, her research concerns interactions between large-scale structures and small-scale turbulence. You can find her on Twitter @FodorKatherine where, in addition to science, she also tweets about cycling.”
Katherine Fodor is a PhD. candidate at the Max Planck Institute for Meteorology in Hamburg, Germany. She uses very high resolution computer simulations to study turbulence in the atmosphere. In particular, her research concerns interactions between large-scale structures and small-scale turbulence. You can find her on Twitter @FodorKatherine where, in addition to science, she also tweets about cycling.”







Salma umer
Hello everyone!
Well, this blog has helped me and made me clear to many points.
I suggest EGU BLOGS to add some kind of information about the atmosphere of the earth and also discuss about the layers of the atmosphere.