Let’s continue the journey of discovering cool facts about sea ice which started with breaking the ice. This time, we’re diving into a fascinating part of the Arctic and Antarctic: the Marginal Ice Zone (MIZ). Imagine a place where the vast, frozen world of sea ice meets the moving waters of the ocean underneath. This is the MIZ, a unique area where air, water, and ice mix and mingle. ItR ...[Read More]
A journey to the Edge of the Ice: Discovering How the Ocean Meets the Polar Sea Ice
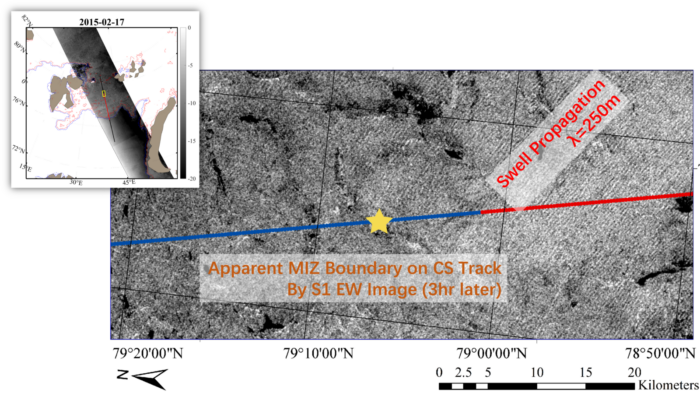
Figure 1: Sentinel-1 image (EW swath mode) of the Marginal Ice Zone case in the Barents Sea on 2015-Feb-17. The CryoSat-2(CS2) track (black) and the retrieved alongtrack Marginal Ice Zone are shown (red). Wave-like structure is observed by Sentinel-1 (3-hr later than CS2). [Adapted from Zhu et al., 2023].
