April Wright recently published a cool paper looking at how to bring morphological analyses of evolutionary relationships into the Bayesian realm. This is her take on it – enjoy! 

Author Bio: My name is April Wright, and I’m a graduate student in David Hillis’ lab at the University of Texas at Austin. I’m largely interested in the estimation and use of phylogenetic trees to answer questions about evolution. Particularly, I’m investigating how we can make the best possible use of our fossils in an era increasingly dominated by genome-scale data. You might say I’m a little bit of a ‘small data’ scientist, though my questions often involve a multitude of small data sets.

Today I’d like to talk a little bit about a recent paper I published as part of my PhD thesis work.

What We Did

We performed a bunch of simulations of morphological data sets to look at whether parsimony or likelihood-based phylogenetic analyses perform better. This is important, as the majority of current morphological analyses exclusively use parsimony. We used an empirical tree borrowed from a 2011 paper by Alex Pyron (see Figure One), and simulated matrices of characters along said tree. We picked this tree because it reflects the complexity of many paleontological trees: extinction events resulting in short tips, mixes of long and short branches, and polytomies where evolutionary relationships are unresolved.

From our data sets, we simulated distributions of missing data by removing characters from our matrices. We don’t expect every character to have an equal probabilty of preservation. We might expect that fast-evolving characters, like digits, to be lost more easily, for example. So we imposed biased missing data to look at the impact of systemically underrepresenting certain characters.

We built trees using the Mk model in MrBayes (for Bayesian trees) and PAUP (for parsimony trees). We used the Robinson-Foulds metric (a measure of distance between different trees) to compare how many nodes in each tree were incorrectly estimated.

What We Found

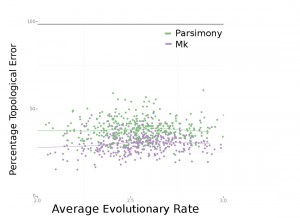
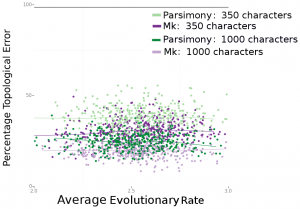
Consistently, Bayesian estimation performed better. In Figure 4 (below), we can see that Bayesian estimation pretty consistently produces less errors than parsimony. In Figure 6 (below), we can see that this result is more striking in smaller data sets. We also found, per Figure 5 in the paper, that the characters that are missing makes a big difference. Missing fast-evolving characters, which display parallelisms and reversals, is not as harmful as missing slower characters, which are more parsimony-informative. This is not too surprising, but characters that display homoplasy provide background information on the overall rate of evolution in the tree and other parameters in likelihood-based analysis. They are still informative under likelihood-based analyses.

Figure 4. Source: Wright and Hillis (2014) – click for larger

Practical Recommendations

Our results suggest a few practical steps for paleontologists.

• Bayesian models are worth learning to use.
  • The effect of using Bayesian analysis is not as effective at reducing error as increasing the number of characters. But it is effective at improving the accuracy of phylogenetic estimation.
• It’s important to pay attention not just to what data you have, but what data are missing. Missing data have been a hot topic in phylogeny for ages. Does it matter? Does it not? Our answer is a clear ‘Yes, missing data matter’. But under-representation of some characters is worse than others.

Figure 6. Source: Wright and Hillis (2014).

The Future

The other two parts of my thesis are also about morphology. One, which will be in review soon, focuses on the use of hyperpriors to relax some of the assumptions of the Bayesian model for topology estimation from discrete morphological data. This study uses empirical data sets to locate situations in which more complex models of character evolution fit the data better, and uses simulations to assess if better model fit translates into more accurate estimation. I’m also working on techniques to discover appropriate partition schemes in morphological data sets. Partitioning allows us to estimate different model parameters for different subset of our data.

We certainly look forward to all of this in the future from April! In the mean time, if you have any comments, please do leave them below.