The human lifespan is too short compared to the geological time. To comprehend long-term phenomena, numerical modeling emerges as an imperative approach. But, there are several ways for visualizing the output of these models. Among these, animations stand out as a powerful tool, allowing us to watch the dynamic evolution of our planet over geological epochs like a movie. Our lives are too short co ...[Read More]
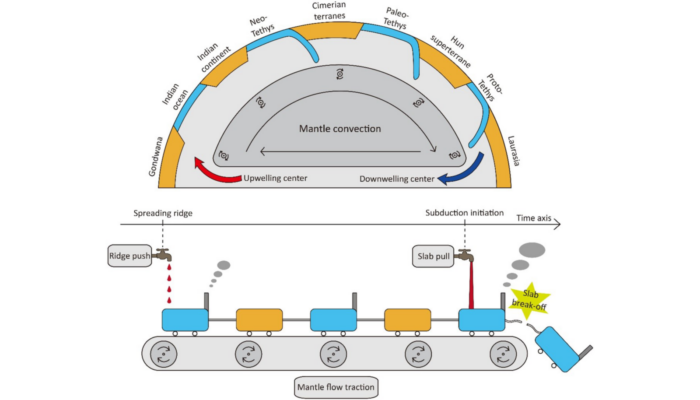
Multiengine-driving Tethyan evolution
The highest mountain range in the Alps in the Western Europe, the towering peaks of the Himalayas in Asia, and ~1/3 world crude oil production in the middle east – what brings these remarkable nature gift together? The answer is Tethyan orogenic belt, which spans across the entire Eurasian continent. This week, we are privileged to have Prof. Zhong-Hai Li from the University of Chinese Academy of ...[Read More]
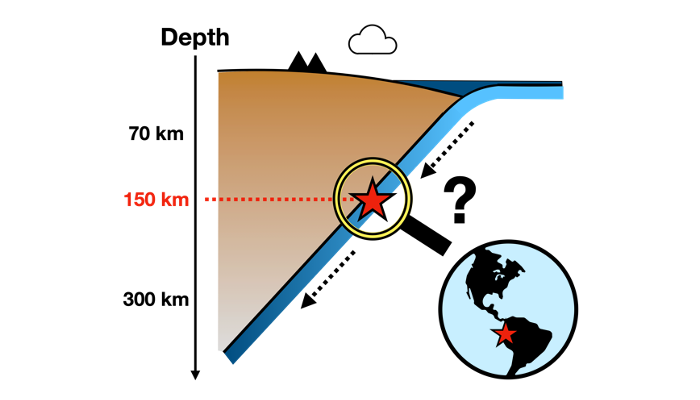
Exploration of Deep Earthquakes and Planetary Interiors
Most earthquakes on Earth start in the shallow, brittle part of the planet. However, there are several regions where earthquakes happen deep in the mantle. Where are these regions? Why do these earthquakes get so deep? In this week’s blog post, Ayako Tsuchiyama from the Massachusetts Institute of Technology (MIT) takes us on a journey into the mysterious world of deep earthquakes. Growing u ...[Read More]
Mantle, Mountains and Molluscs
Geodynamic models and landscape evolution models are becoming important tools to quantify the formation and development of paleogeographic features, contributing to our understanding of the patterns of biodiversity evolution. Earth, a dynamic system The Earth’s surface works as a dynamic system and is continuously sculpted through the geological timescale by weathering, wind, rivers, and many othe ...[Read More]